[Communicating science series]
[Gobbledygook ahoy, PopSci call-outs, …]

“Can particles really be in two places at once?“

So remote from everyday experience: How to describe physical behavior that human communication never evolved to describe? To describe something that the mere act of observation extinguishes?

Use an abstract symbolic framework like mathematics? And then “convert” mathematical expressions into standard language? Maybe try to be more precise? Can that ever be “correct,” or even make sense? Gobbledygook.

In trying to communicate key concepts of quantum theory (like superposition and entanglement) using “PopSci language” [1], do the phrases “in two places at once” and “in two states at once” make any sense?

Interestingly, in her video (below) regarding the “Can particles really be in two places at once?” question, Hossenfelder never actually addresses the “places” aspect. She talks about a particle’s [qubit’s] state. But in quantum physics, a particle’s position is an observable of a state / wave function (ket).

Today I want to talk to you about what happened when I wrote an opinion piece for the Guardian about quantum computing, had to explain what a qubit is, and decided against using the phrase that it “can be in two states at the same time.”

By writing this I wanted to get across two points. First, the phrase that “a qubit can be in two states at the same time” … makes no sense and would in my opinion better be avoided. Second, it’s the entanglement that makes the difference between a conventional computer and a quantum computer.

I still think that the explanation that I gave for a quantum bit was more truthful to the mathematics than the more commonly used phrase that it can be in “two states at once.”

How would you know that a particle is in two places at once? In principle (i.e, without observation)? – in the sense that it’s not in any one place. Or, in fact via measurement at a particular time?

My take is that it’s not correct to say that a particle (e.g., an electron) can be in “two places at once” – rather than in a superposition of two states – of two wave functions (kets) for position. [3] [4]

A particle’s (localized field excitation’s) extension in space – real and Hilbert – entails an indeterminate, probablistic position. It’s not in two (or more) places at once. That’s why quantum physics is weird. [5]

Modern quantum theory describes electrons being more like fuzzy waves, like taking an electron and smearing it out into a strange ‘probability distribution’ in which the actual electron is a ghost, existing in many places and nowhere in particular all at once. – The Invisible Universe: Why There’s More to Reality than Meets the Eye by Matthew Bothwell

Instead of picturing a hard, solid, precise point in space and time, scientists now see a particle as a cloud of fuzzy probabilities … quantum states. – Paul Sutter, “Quantum Weirdness May Seem to Outrun Light — Here’s Why It Can’t” (September 29, 2018)

---

• Blogspot > Backreaction > “Can particles really be in two places at once?” by Sabine Hossenfelder (June 11, 2022)

… our language isn’t fit to describe something we cannot experience.

We’ve never needed the language to explain quantum behavior so we don’t have it.

• YouTube > Sabine Hossenfelder > “Can particles really be in two places at once?” (June 11, 2022)

[Excerpts]

I believe the problem is that when we write about quantum mechanics we’re faced with the task of converting mathematical expressions into language. And regardless of which language we use, … our language didn’t evolve to describe quantum behavior. So all the words that we can come up with will be wrong and will be misleading. There’s no way to get it right. [2]

What’s a superposition? A superposition is a sum of vectors in a Hilbert space. Alright. But if one of the vectors is a particle going left and the other a particle going right, what does this superposition mean? I don’t know. Could you say it’s a particle going into both directions? I guess you could say that. I mean, you just said it, so arguably you can. But is that what it actually is? I don’t think so.

For one it’d be more accurate to say that the wave-function “describes” a particle instead of saying that it “is” a particle.

But maybe more importantly, I don’t think such a superposition is anything in the space we inhabit. It’s a vector in this mathematical structure we call the Hilbert space. And what does that mean? I don’t know. I don’t think there are any words in our language to explain what it “means”.

When it comes to quantum mechanics, I think what will happen in the long run is that the mathematical expressions will just become better known and we will use them more widely.

Like we’ve become used to talking about electromagnetic radiation. That was once a highly abstract mathematical concept, waves that travel through empty space, rather than traveling in some medium. But we now use electromagnetic radiation so frequently that it’s become part of our everyday language.

I think that it’ll go the same way with qubits and superpositions.

Terms

Qubit
Quantum advantage

Superposition

Quantum superposition is a fundamental principle of quantum mechanics. … that every quantum state can be represented as a sum of two or more other distinct states. … a qubit may be in a superposition of both states [namely, the basis states].

Hilbert space
Complex number
State space
Bloch sphere

Wave function

• Quanta Magazine > “Entanglement Made Simple” by Frank Wilczek (April 28, 2016): “… In quantum theory, states are described by mathematical objects called wave functions.”

Basis vector
Electromagnetic radiation

Bra–ket notation [6]

Notes

[1] Wiki: Popular science – popsci as particularly for these threads:

1. Generalized, simplified science concepts
2. Presented for an audience with little or no science background, hence explaining general concepts more thoroughly
3. Use of metaphors and analogies to explain difficult or abstract scientific concepts

[2] This 2021 interview provides background on Hossenfelder’s “Science without the gobbledygook” channel.

• Nautil.us > “Talking Pop Science with Physicist Sabine Hossenfelder” by Brian Gallagher (July 14, 2021)

[3] Compare this Quora thread, where words in [ ]’s are mine.

• Quora > “In quantum physics are there particles that can be in multiple places at the same time?” by Viktor T. Toth (2019)

In classical physics, a particle always has a well-defined position [a definite trajectory]. In quantum physics, a particle’s state is defined by what is called a superposition of positions. That is to say, it is a weighted mixture of all possible positions [within the specified, isolated system].

When we measure the position of a particle, we get one result. However, the equations don’t tell us which result it will be. They only give us probabilities. The coefficients, or weights, in that superposition tell us how probable various positions are.

A measurement will always find a particle at a specific location. You will never catch the particle in two places at once. However, between measurements, a particle [localized field excitation] can be in two (or more) places at once [the excitation is extended in space]. The famous experiment here is the so-called two-slit experiment, which allows an electron to go through a barrier that has two holes. Detecting electrons on the other side tells us the story: Each electron [field excitation] goes through [interacts with] both slits, and then these two “potentialities” (for lack of a better word) proceed to interfere [superpose] with each other , determining ultimately where the electron will be detected.

So yes, in quantum physics particles are in multiple places at once [localized field excitations are extended in space], but do not think of them as miniature cannonballs sprouting clones. Rather, between measurements, a particle has no well-defined position, only this superposition business that ultimately determines the probability of finding the particle at various locations. When we measure the particle, we only ever measure the one particle, and at the moment of measurement, it will have a well-defined location.

Compare that to Wiki‘s note regarding the double-slit experiment:

One practical example of superposition is the double-slit experiment, in which superposition leads to quantum interference. The photon state is a superposition of two different states, one corresponding to the photon travel through the left slit, and the other corresponding to travel through the right slit. The relative phase of those two states depends on the difference of the distances from the two slits. Depending on that phase, the interference is constructive at some locations and destructive in others, creating the interference pattern. We may say that superposed states are in coherent superposition, by analogy with coherence in other wave phenomena.

[4] Consider this explanation of superposition vs. entanglement, where words in [ ]’s are mine.

• Byjus > “What is the difference between superposition and entanglement?” (Date unknown)

The primary difference between quantum entanglement and quantum superposition is that quantum entanglement involves the exchange of [correlation of] quantum information between two particles at a distance, while quantum superposition involves the uncertainty of a particle [localized field excitation] (or multiple particles) being in several states [with indefinte aspect] at one point of time.

And compare that to what Hossenfelder said:

What’s a superposition? A superposition is a sum of vectors in a Hilbert space. Alright. But if one of the vectors is a particle going left and the other a particle going right, what does this superposition mean? I don’t know. Could you say it’s a particle going into both directions? I guess you could say that. I mean, you just said it, so arguably you can. But is that what it actually is? I don’t think so.

For one it’d be more accurate to say that the wave-function “describes” a particle instead of saying that it “is” a particle. But maybe more importantly, I don’t think such a superposition is anything in the space we inhabit. It’s a vector in this mathematical structure we call the Hilbert space. And what does that mean? I don’t know. I don’t think there are any words in our language to explain what it “means”.

[5] Compare the language in this 2014 article re nonlocality.

• “Experimental Proof of Nonlocal Wavefunction Collapse for a Single Particle Using Homodyne Measurement” (December 30, 2014)

A single quantum particle can be described by a wavefunction that spreads over arbitrarily large distances, but it is never detected in two (or more) places. This strange phenomenon is explained in quantum theory by what Einstein repudiated as “spooky action at a distance”: the instantaneous nonlocal collapse [update] of the wavefunction to wherever the particle is detected. We demonstrate this single-particle spooky action, for the first time with no efficiency loophole, by splitting a single photon between two laboratories and experimentally testing if the choice of measurement in one lab really causes a change in the local quantum state in the other lab.

[6] How to write kets. An example.

• Quora > “Can quantum entanglement be visualized“

Jayadev Vijayan
An imploring explorer Updated 8y [2014]
Your visualization as given in the description? – No!

First of all, passing through a beam splitter does not entangle the spins of the photons!

Secondly, a beam splitter does not ‘split’ individual photons. You can never have entanglement with just one photon!

What happens when a single photon is incident on a beam splitter is as follows:

Assuming the beam splitter is made of a material that is equally reflective and transmittive (50-50 beam splitter), this means that when a single photon is incident on this beam splitter, it is equally likely to get reflected or transmitted. Note that the photon does NOT split into two making one half reflect and the other half transmit. So in roughly half the number of trials, the single photon will get transmitted and the half the number of time it will get reflected.

If you really want to write a superposition state for this photon after it passes through the beam splitter, it is as follows:

|psi> = (1/sqrt(2)) [ |transmitted> + |reflected> ]

So if the beam splitter is arranged such that the transmitted ray goes to the right and the reflected ray to the left, the superposition is:

|psi> = (1/sqrt(2)) [ |right> + |left> ]

Or, equivalently, if you were to measure from only either the left side or the right side:

|psi> = (1/sqrt(2)) [ |there> + |not there> ]

where the (1/sqrt(2)) comes because I assumed a 50-50 beam splitter. [So, the sum of the squares of the coefficients = 1.]

And this state can apparently be visualized like this …

This is the Wigner function of ‘Schrodinger kitten states’. I don’t know how exactly this is obtained. Maybe someone more knowledgeable can help!

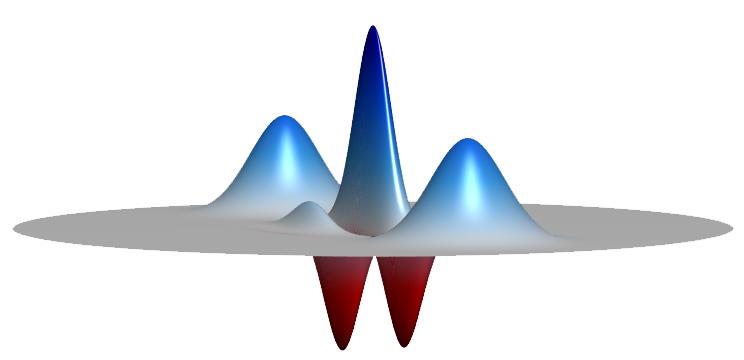
Here’s another visualization.

• Wiki > Commons > File > Cat state wigner function (10 August 2017)

Description: The iconic textbook example of a Wigner function for a Schrödinger cat state.

The bell shapes represent the “alive” and “dead” possible states for the “cat” and the oscillations between them indicate the quantum coherence between these states (i.e., the classic “both alive and dead” statement).

A similar Wigner function without these interference terms would represent a state with a classical coin toss probability of being either alive or dead but not both.

The presence of the interference terms indicates that this Wigner function represents a state that is in both states (“alive and dead”) at the same time (a superposition).